The Key Material Characteristics that Enable Pipe Deflection
This post was originally published in December of 2017, but has been updated to be more comprehensive, including a video of CPVC during a flattening test.
Linear expansion is an unavoidable phenomenon that affects all piping material—including both metals and plastics. If a run of pipe is constrained at both ends, an increase in temperature will cause the material to expand, resulting in compressive stress. When this mounting force exceeds the material’s allowable stress, damage occurs to the piping system.
During piping system design, architects and engineers must build in expansion loops to deflect this compression stress. In each of the three types, a right angle is required.
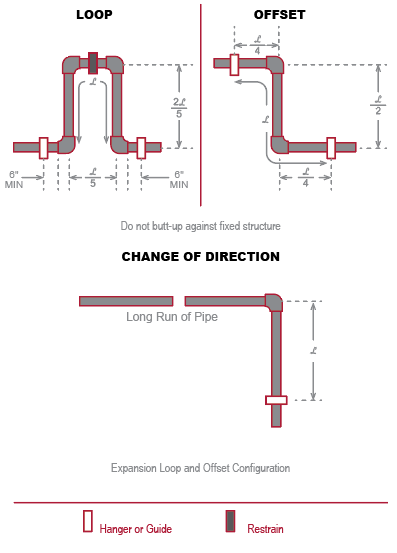
Expansion loops, expansion offsets and changes of direction provide a linear direction for the pipe to move. But, which characteristics of the material enable it to deflect without causing damage to the pipe?
To learn how to account for thermal expansion in piping system design, check out our previous post on that topic.
What Two Material Characteristics Allow the Pipe to Deflect for Expansion Loops?
Each loop relies on the pipe’s ability to deflect without sustaining damage. There are two key material characteristics that make this possible.
1. Flexural Modulus of Elasticity
A piping material’s flexural modulus of elasticity demonstrates how much stress can be put on a material before it can no longer return to its original state. Essentially, it is a ratio of stress to strain.
When stress acts on the material, a certain amount of strain—or deformation—takes place. As the stress acting on the material increases, so does the strain. At a certain point, the strain is too great, damaging the material.
Stiffer materials have a higher modulus of elasticity. No matter how stiff the material, the modulus of elasticity will decrease as temperature increases—meaning the higher the temperature, the easier the pipe will deflect.
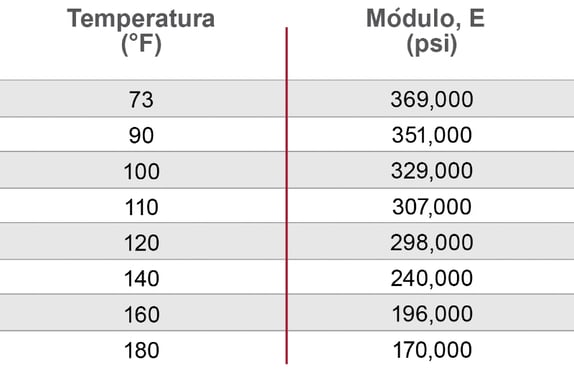
The chart displays the flexural modulus of elasticity for Corzan® CPVC at different temperature.
The modulus of elasticity is a property of the material, and is defined using the ASTM D790 Standard Test Method for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials. This standard explains how to prepare specimens and set up a three-point loading system to determine the flexural properties of plastic materials. During this test, a load is placed on the specimen. Flexural stress is calculated from the load-deflection curve. The resulting stress vs. strain curve is used to determine several properties:
- The linear portion of this curve is the elastic region, which is the range where the material will retain its properties after a load is removed.
- The modulus of elasticity is the slope of this region.
2. Working Stress
Working stress is the maximum allowable stress a material can be subjected to while in use. At a certain stress level, materials will sacrifice structural integrity. All materials exhibit different levels of working stress and the value is dependent on the geometry of the material and the working temperature.
The geometry of a material is the final form the compound takes on. For example, CPVC compound can be manufactured into schedule 40 and schedule 80 piping, custom molded into fittings, and fabricated into ducting or liners. Each geometry will exhibit a different working stress.
Similar to modulus of elasticity, working stress is also dependent on the temperature of an application. The maximum allowable working stress decreases as temperature increases.
As shown in the chart below, Corzan CPVC can handle greater maximum stress at lower temperatures than at higher temperatures.
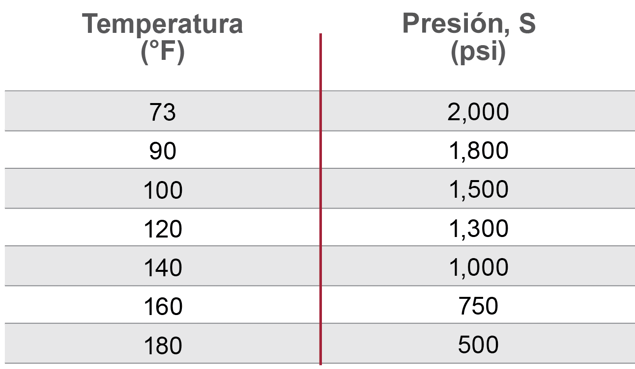
The chart displays the working stress of Corzan CPVC at different temperature.
Working stress is a defined value for each material and geometry, and the ASTM D1598 Standard Test Method for Time-to-Failure of Plastic Pipe Under Constant Internal Pressure is the method for testing and calculating the hoop stress (or working stress) of the longitudinal stress arising from pressure on the pipe.
Not part of the expansion loop formula discussed below, but an important aspect of stress that piping must overcome to deflect safely is compressive stress. To understand how a pipe will respond to stress during compression, a flattening test can be employed. Outlined in ASTM F441, a pipe should flatten until the distance is 40% of the original diameter without splitting or cracking during the flattening test. Corzan CPVC, as the video below shows, flattens 100% without adverse affects.
Corzan® CPVC Flattening Test
Expansion Loop Formula: Tying These Together
To determine the linear expansion of a pipe and the necessary dimension of an expansion loop, designers use the Expansion Loop Formula. The characteristics of a piping material covered above—the modulus of elasticity and working stress—make up half of the equation.
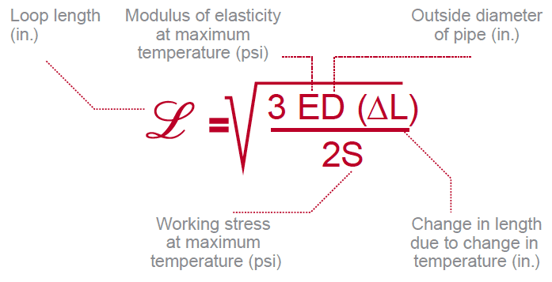
Here’s how each variable impacts the length of the expansion loop:
- Flexural modulus of elasticity at the maximum temperature (E): As the modulus of elasticity increases, so does the required length of the expansion loop. When equal forces are applied to pipes of the same diameter, the stiffer pipe will require a longer length to deflect the same distance as the more flexible pipe.
- Working stress at the maximum temperature (S): As working stress increases, the necessary loop length decreases. In other words, the more stress the pipe can sustain, the less of an area the applied force from deflection needs to be spread across.
- Change in length due to change in temperature (∆L): This change in length is calculated by the thermal expansion formula, which takes into account the length of the pipe, the change in temperature and the material’s coefficient of thermal expansion. As this value increases, the required length of the expansion loop also increases.
- Outside diameter of the pipe (D): As the outside diameter of the pipe increases, the required loop length also increases. A wider pipe is less flexible, and needs more length of pipe to deflect across.
Calculate the Loop Length Required for Your System
To help engineers in the designing of Corzan® CPVC piping systems, we developed a Pipe Expansion Calculator. If you know the pipe diameter, maximum and minimum temperatures, and pipe run length, the calculator will provide the loop lengths required for your system.


